Predicting sequences of vectors (regression) in Keras using RNN - LSTM
Update (24. 03. 2017): My dear friend Tomas Trnka rewrote the code below for Keras 2.0! Check it on his github repo!
Update (28.11.2015): This article become quite popular, probably because it's just one of few on the internet (even thought it's getting better). Please read the comments where some readers highlights potential problems of my approach. Furthermore I am afraid I can't help you with your specific cases, since I don't work with LSTM any more. And, to be honest, I don't really feel very confident about my understanding to LSTM to give advices. This is just what worked for me.
My task was to predict sequences of real numbers vectors based on the previous ones. This task is made for RNN. As you can read in my other post Choosing framework for building Neural Networks (mainly RRN - LSTM), I decided to use Keras framework for this job.
Coding LSTM in Keras
CAUTION! This code doesn't work with the version of Keras higher then 0.1.3 probably because of some changes in syntax here and here. For that reason you need to install older version 0.1.3. To do that you can use pip install keras==0.1.3 (probably in new virtualenv). For this tutorial you also need pandas. Please let me know if you make it work with new syntax so I can update the post.
Example code for this article can be found in this gist. This is tested on keras 0.1.3. It is edited a bit so it's bearable to run it on common CPU in minutes (~10 minutes on my laptop with i5). When you plot the results from resulted .csv files you should get something like this:
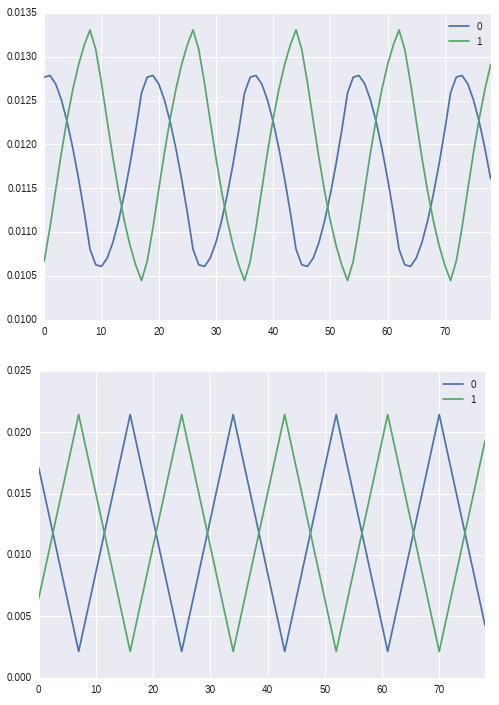 where predicted points are up and true data down.
where predicted points are up and true data down.
Quick hands-on
To run the script just use python keras.py. It will create two csv files (predicted.csv and test_data.csv) which should be almost same.
Step-by-step solution
Keras have pretty simple syntax and you just stack layers and their tuning parameters together.Let's build our first LSTM.
The code is as follows:
from keras.models import Sequential
from keras.layers.core import Dense, Activation
from keras.layers.recurrent import LSTM
in_out_neurons = 2
hidden_neurons = 300
model = Sequential()
model.add(LSTM(in_out_neurons, hidden_neurons, return_sequences=False))
model.add(Dense(hidden_neurons, in_out_neurons))
model.add(Activation("linear"))
model.compile(loss="mean_squared_error", optimizer="rmsprop")
and that's it! We just created LSTM NN which expects vector of length 2 and NN has 1 leayer with 300 hidden neurons. It returns vector of length 2 (this doesn't have to be the same in your case, but for my purposes it is).
Data preparation
Now we need to prepare data. Let's generate some randomly (you need pandas library for this example). Imagine that we have two stocks and we have prices for every minute.
import pandas as pd
from random import random
flow = (list(range(1,10,1)) + list(range(10,1,-1)))*1000
pdata = pd.DataFrame({"a":flow, "b":flow})
pdata.b = pdata.b.shift(9)
data = pdata.iloc[10:] * random() # some noise
this will create the saw-like columns shifted to each other.
Now it's critical to decide how far our network will see to the history. In other words, how much vectors you let the network to prime on before it predicts the another one. Let's say we will use 100 vectors for priming. One input element will hence be a matrix of 100 rows and 2 columns.
If we think about our data as two stocks, than every row corresponds to one minute and we let network to be primed based on 100 previous minutes. So let's say we feed in prices of 100 (true) minutes and we want to predict the 101th minute. Then we feed in prices for second to 101th minute (the 101th minute is the true one, not the one predicted from the previous step) and let it predict the 102th and so on.
So how to transform the data to our format? As an input X we want array of n matrices, each with 100 rows and 2 columns (technically, X is a tensor with dimensions n x 100 x 2). The target y will be matrix n x 2 - for each input X_i (matrix 100 x 2) we want one corresponding row of y (with just two elements).
Below is the function which does exactly what we want. Plus, there is one more function which will split our data into train and test data.
import numpy as np
def _load_data(data, n_prev = 100):
"""
data should be pd.DataFrame()
"""
docX, docY = [], []
for i in range(len(data)-n_prev):
docX.append(data.iloc[i:i+n_prev].as_matrix())
docY.append(data.iloc[i+n_prev].as_matrix())
alsX = np.array(docX)
alsY = np.array(docY)
return alsX, alsY
def train_test_split(df, test_size=0.1):
"""
This just splits data to training and testing parts
"""
ntrn = round(len(df) * (1 - test_size))
X_train, y_train = _load_data(df.iloc[0:ntrn])
X_test, y_test = _load_data(df.iloc[ntrn:])
return (X_train, y_train), (X_test, y_test)
Ok, now we have the data. Let's retrieve them and fit the model:
(X_train, y_train), (X_test, y_test) = train_test_split(data) # retrieve data
# and now train the model
# batch_size should be appropriate to your memory size
# number of epochs should be higher for real world problems
model.fit(X_train, y_train, batch_size=450, nb_epoch=10, validation_split=0.05)
after you fit the model, you can predict the sequences using predict. Let's compute rmse for the predicted values and the true values.
predicted = model.predict(X_test)
rmse = np.sqrt(((predicted - y_test) ** 2).mean(axis=0))
# and maybe plot it
pd.DataFrame(predicted[:100]).plot()
pd.DataFrame(y_test[:100]).plot()
The plots should be almost exactly the same. E.g. here is an example trained on first 10000 training data. Dashed lines are predicted values.
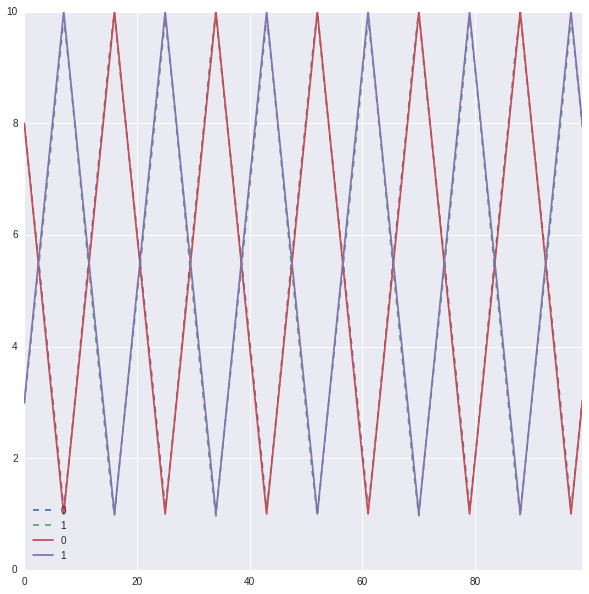
Adding more layers and dropouts
You can of course create more complicated structures. There is a difference in keyword return_sequences. This should be changed to True when passing to another LSTM network. Let's create LSTM with three LSTM layers with 300, 500 and 200 hidden neurons respectively. It will take vector of length 5 and return vector of length 3. As you can see, there is also dropout.
from keras.models import Sequential
from keras.layers.core import Dense, Activation, Droupout
from keras.layers.recurrent import LSTM
model = Sequential()
model.add(LSTM(5, 300, return_sequences=True))
model.add(LSTM(300, 500, return_sequences=True))
model.add(Dropout(0.2))
model.add(LSTM(500, 200, return_sequences=False))
model.add(Dropout(0.2))
model.add(Dense(200, 3))
model.add(Activation("linear"))
model.compile(loss="mean_squared_error", optimizer="rmsprop")
Limitations and embedding layer from Keras
As you probably realized, the proposed solution is quite inefficient, since there is huge redundancy in data. I haven't figure out how to do it easily though...
It should be mentioned that there is embedding layer build in keras framework. Unfortunately, the example there is given only for categorical case and I haven't found a way how to use it for this continuous application.
Your contribution
Please feel free to make any suggestions so I can tweak the article. Furthermore, if your code isn't private and can be publicly shared, leave a comment with gist link so I can list it below. Let help each other!